What is a Trigonometry Table?
A trigonometry table is a chart listing the values of six primary trigonometric ratios for standard angles 0°, 30°, 45°, 60°, and 90°. These ratios are:
- Sine (sin θ)
- Cosine (cos θ)
- Tangent (tan θ)
- Cotangent (cot θ)
- Secant (sec θ)
- Cosecant (cosec θ)
It is a quick reference tool used in mathematics, physics, engineering, and real-life applications. Students use it to solve triangle, height-distance, and angle-related problems efficiently.
Also Read: What is ozone and how does it affect any ecosystem?
Table of Contents
Trigonometric Ratios Explained
The six primary trigonometric functions are derived from a right-angled triangle:
| Function | Formula |
|---|---|
| sin θ | Opposite / Hypotenuse |
| cos θ | Adjacent / Hypotenuse |
| tan θ | Opposite / Adjacent |
| cot θ | 1 / tan θ |
| sec θ | 1 / cos θ |
| cosec θ | 1 / sin θ |
These ratios form the foundation of all trigonometry problems.
Complete Trigonometry Table (0° to 90°)
| Angle (°) | sin θ | cos θ | tan θ | cot θ | sec θ | cosec θ |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | ∞ | 0 | ∞ | 1 |
Tip: Keep this table handy while solving problems to memorize values effectively.
How to Memorize the Trigonometry Table Easily
1. Square Root Trick for Sine
The sine values for standard angles can be memorized as:
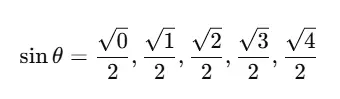
2. Complementary Angle Identities
- Cosine: cos θ = sin (90° − θ)
- Tangent: tan θ = sin θ / cos θ
- Cotangent: cot θ = 1 / tan θ
- Secant: sec θ = 1 / cos θ
- Cosecant: cosec θ = 1 / sin θ
3. Hand Trick for Quick Reference
Fold the finger corresponding to the angle (0°, 30°, 45°, 60°, 90°):
- Sine: Count fingers below → √(fingers)/2
- Cosine: Count fingers above → √(fingers)/2
This visual trick helps students memorize values quickly.
Applications of the Trigonometry Table
Mathematics
- Solving right-angled triangles
- Height and distance problems
- Coordinate geometry applications
Physics
- Calculating angles of incidence and reflection
- Analyzing motion, forces, and vectors
Engineering
- Designing bridges, ramps, and mechanical structures
- Calculating load and stress angles
Astronomy
- Measuring distances between celestial objects
- Satellite navigation and astronomy calculations
Real-Life Examples of trignometry
- Surveyors measure land elevation and plot areas.
- Architects calculate slopes of roofs, stairs, and ramps.
- Navigators and pilots determine directions and locations.
- Engineers design systems based on precise angles and forces.
Trigonometry is not just academic; it is applied in real-world problem solving.
Common Mistakes to Avoid
- Confusing sine and cosine values
- Using degree mode instead of radian mode on calculators
- Forgetting undefined values like tan 90° or sec 90°
- Not applying trigonometric identities properly
Practice and daily revision reduce mistakes.
FAQs About Trigonometry Table
Q1: What is a trigonometry table?
A: A chart showing values of sin, cos, tan, cot, sec, and cosec for standard angles.
Q2: How can I memorize it easily?
A: Use the square root trick, complementary angle identities, and the hand trick.
Q3: Why is the trigonometry table important?
A: It helps solve triangle, height-distance, and real-life problems faster and accurately.
Q4: Can I use it in exams?
A: Yes, students are often expected to recall values from memory.
Q5: What are the standard angles in the table?
A: 0°, 30°, 45°, 60°, and 90°.
Final Tips to Master the Trigonometry Table
- Daily Practice: Solve problems using the table regularly.
- Visual Memorization: Use the hand trick or flashcards.
- Real-Life Application: Observe angles in buildings, roofs, and ramps.
- Mnemonics: Create simple rhymes to remember values.
- Regular Revision: Keep the table handy for quick review before exams.
